Written by Dr Swaminathan Krishnan, Senior Data Scientist, Illumination Works

Data science reflects on the past to illuminate the future, but since humans make decisions based on their assessment of risks and rewards, it is crucial that this forecast is accompanied by a measure of the degree to which it can be relied upon, in other words, an uncertainty metric.

Information is the Resolution of Uncertainty

“Information is the Resolution of Uncertainty,” a phrase famously attributed to Claude Shannon, alludes to the fact that the presence of noise in data distorts information and introduces uncertainty into how this data is interpreted, while a reduction of the noise in the data brings information to the fore, helping to resolve this uncertainty and better revealing the underlying truth of the data.

These ideas, first published in a 1948 Bell System Technical Journal paper, revolutionized communication or information theory and immediately impacted science, engineering, business, and economics. They underpin uncertainty quantification in data science, a critical cog in the engine of human decision-making.

Article Highlights

• Decisions Have Consequences
• Types of Uncertainty
  • Aleatoric Uncertainty
  • Epistemic Uncertainty
• Quantifying Uncertainty
  • Bayesian Modeling
  • Uncertainty Representation

In Part 1 of this two-part article, Dr. Krishnan, Senior Data Scientist at Illumination Works, discusses uncertainty and how predictive and insightful artificial intelligence/machine learning (AI/ML) applications can bracket outputs/insights with uncertainty bounds, allowing users to understand how much credence to place on a model’s outputs for decision making.

Article Highlights

• Decisions Have Consequences
• Types of Uncertainty
  • Aleatoric Uncertainty
  • Epistemic Uncertainty
• Quantifying Uncertainty
  • Bayesian Modeling
  • Uncertainty Representation

These ideas, first published in a 1948 Bell System Technical Journal paper, revolutionized communication or information theory and immediately impacted science, engineering, business, and economics. They underpin uncertainty quantification in data science, a critical cog in the engine of human decision-making.

In Part 1 of this two-part article, Dr. Krishnan, Senior Data Scientist at Illumination Works, discusses uncertainty and how predictive and insightful artificial intelligence/machine learning (AI/ML) applications can bracket outputs/insights with uncertainty bounds, allowing users to understand how much credence to place on a model’s outputs for decision making.

Every Choice Counts: Decisions Have Consequences 

Consider this Real-Life Scenario: You are considering a trip to Europe with your family. You want to make sure the trip ends up being a truly memorable one for your wife and kids. You know it is going to break the bank and want to make each day count. Are you going to pick winter break, spring break, or summer for the trip?

Of the three choices, there is greatest uncertainty with the choice of spring break. If all goes well, you will have the most perfect spring-like weather, and your vacation will be a dream vacation. On the other hand, while you may have planned spring-suitable activities, all your plans could go haywire if wintry or summery weather strikes. While the upside returns of a wonderful spring in Europe could be tempting, are the downside outcome of your plans going haywire worth it?

Probability of Perfect Weather. To make an informed decision on this, you may want to know what the chances of unplanned weather striking are. You may look up the data from the last few years and be tempted to take the average to be indicative of what you can expect for this year. But that metric alone hides important details. Wildly swinging temperatures and mildly varying temperatures could both result in the same average, yet the upside and downside returns for these two premises are vastly different, and hence important to consider when making your decision. In the latter case with mildly varying historical temperatures, you have greater confidence in your estimate for the temperatures you can expect to encounter, whereas in the former case with wildly swinging temperatures, you are less certain that the temperatures you expect to encounter will remain close to the average historical temperature. The large deviations from the average in the historical temperatures have made your estimate/forecast/prediction for the future temperatures highly uncertain. The greater this uncertainty, the less likely you are to go with the choice of spring break for your vacation.

What About Business Decisions? Just as each of us inherently uses the notion of uncertainty in our daily lives, so too in businesses, decisions are made accounting for upside and downside risks and returns. While this is often done informally and placed under the vast fuzzy umbrella of business insights and heuristics, formally quantifying uncertainty can facilitate rational decision making that results in more definitive and reliable business outcomes. Today, data scientists develop AI/ML models on the backs of vast amounts of data for a range of applications in several domains such as natural language processing (NLP), computer vision (CV), and time series forecasting, but the best among these are those that quantify the uncertainties associated with the model outputs. Next, let’s look at the notion of uncertainty in data science.

The Hidden Forces Shaping Decisions: Types of Uncertainty

Aleatoric Uncertainty. Consider these questions: How much volatility/noisiness in data is a model unable to get rid of? How much randomness is baked into the system generating the data? The uncertainty resulting from this inherent randomness in the system is termed aleatoric. Clients care about this. It gives them a feel for how much credence/trust they can place on a model, given the inherent randomness in their data. This information needs to be accounted in their actions going forward involving the model’s predictions. It is important to recognize that aleatoric uncertainty would not be any lower if we had the benefit of more data. No matter how much additional data we collect, the inherent randomness remains and cannot be eliminated or reduced. For example, no model can consistently predict the outcome of a toss of an unbiased coin, no matter how vast the dataset of past outcomes is that the model has been trained on.

Epistemic Uncertainty. Now let’s consider: How well does a model generalize? How well does it do on predictions associated with unseen data, data that it has not been trained on? The uncertainty resulting from the model’s performance on unseen data as compared to its performance on the training data is termed epistemic. In a certain regime of the input parameters, the model may consistently perform well, but in a different regime, it may be inconsistent with its predictions and/or consistently perform poorly simply because the training data did not include data points from that input parameter regime. For example, suppose a car rental company is interested in a forecasting model that would allow them to estimate the number of cars that would be needed at a particular location. It has collected rental data over the last three months, but the data collected was limited to weekdays alone, not weekends. A model trained on this data would do very well in estimating the demand on weekdays, but if the weekend demand is typically significantly different from weekday demand, then it would likely yield poor predictions for weekends. The company cannot rely on the model as much for weekend estimates as for weekday estimates. The resulting uncertainty for weekend estimates is an example of epistemic uncertainty. It can be lowered by simply collecting weekend data over a few months and retraining the model on the more comprehensive dataset covering both weekdays and weekends. In general, clients need to be educated on the limitations of a model so they can limit their use of the model to its range of applicability.

Lowering Epistemic Uncertainty: Unseen Data and Robust Models. Data scientists can lower epistemic uncertainty by collecting greater amounts of data and increasing the data coverage and density. Another approach is to select models that can generalize better, even within the expanse of the data collected. It is common practice in data science to use various unseen data testing methods such as k-fold cross-validation (out-of-sample testing) and regularization and dropout to reduce overfitting to the training data. Another practice is relying on ensemble methods such as bagging, boosting, and stacking to lower model variance and/or bias. For poorly sampled data regimes, or sample data not representative of the population, data scientists may resort to data imputation (filling in the missing values intelligently) using techniques such as simple imputation (substituting missing data with the mean/median/mode/next/previous/maximum/minimum or some other fixed value for continuous variables and the plural for categorical variables), regression imputation (developing regression equations on the available data and using the equations to predict the missing data), K nearest neighbors (weighted average of the values for the K nearest neighbors for which data is available), clustering the available data and classifying the missing data into one of the clusters, predictions from decision trees or random forests developed using available data, multiple imputation [1][2], etc.

The unseen data referenced above could be of two kinds, data that is similar to the training data (data that is generated by the same distribution generating the training data) and data that is distinctly dissimilar [out-of-distribution (OOD) data generated by a distribution distinct from that which the training data was generated]. Uncertainty associated with the former can be more easily characterized by splitting the available data into train and test data sets and computing uncertainty metrics on the test data. Model uncertainty associated with the latter is not only likely to be larger, but it is also likely to be harder to estimate. Can the model identify the fact that an OOD datapoint in fact comes from a distribution that is distinct from that of the training dataset? A model that can is termed a robust model. To check for model robustness, one would need to create an OOD dataset by either perturbing and/or corrupting the test dataset or creating a synthetic OOD dataset if one does not exist [3].

The Numbers Behind the Unknown: Quantifying Uncertainty

Bayesian Modeling. Bayesian modeling is a powerful approach to organically incorporate uncertainty into an estimation/prediction exercise. In simple terms, it involves improving our prior knowledge or understanding of a random process with the information provided by newly collected data to arrive at a higher state of posterior knowledge or understanding through the selection of a probabilistic model (from a set of models) that can best explain the new data collected.

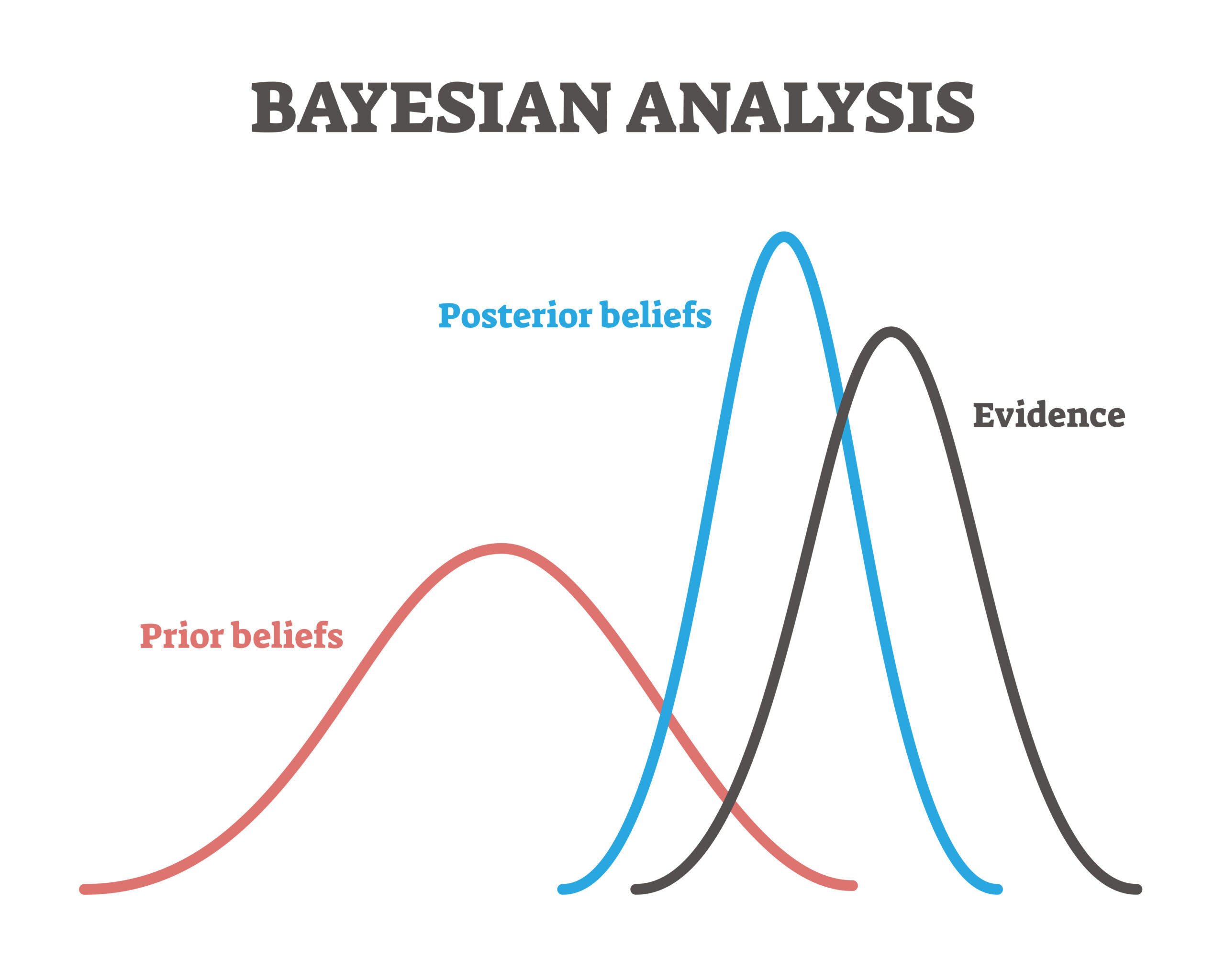
The new stock estimates, informed by the data collected, would be more reliable and allow you to manage your cash flow and storage space better. These would be your posterior estimates that are improved estimates over the prior estimates on the basis of the data collected, which serves as the evidence.

Evidence helps lower epistemic uncertainty. Probability distributions offer a quantitative, yet intuitive, avenue for tracking this uncertainty. One can quickly arrive at the chances of any event or outcome, the kind of insight that all of us routinely use in our daily lives, and use Bayes’ theorem to update prior distributions to posterior distributions in the face of evidence. While classical Bayesian models have historically treated all uncertainty as epistemic through probability distributions on the parameters of the ML model, more recently, researchers have tried tracking aleatoric uncertainty separately from epistemic uncertainty by modeling the probability distribution of the error in the predicted output of the model [4].

Uncertainty Representation. Uncertainty can be expressed as a numerical value (confidence rating), a confidence interval (a range about the prediction), a set of candidate answers, or as a decision to abstain from offering a prediction as in I don’t know [5]. Common evaluation metrics include [6]:

• Calibration – The degree of agreement between the probability of the prediction and the observed frequency of the predicted event in the validation dataset [7]. A calibration curve or a reliability diagram is a plot of the model-predicted probability of an event or a class on the X-axis plotted against the fraction of samples actually belonging to that class in the dataset (the frequentist actual probability of that class) on the Y-axis. The samples are distributed to one of N predicted probability bins based on the predicted probabilities of the points belonging to that class. The center of the probability bin represents the X-coordinate. Within each bin, the fraction of samples that actually belong to that class is the Y-coordinate. The N points determined form the calibration curve. For a perfectly calibrated (fully trustworthy) model, this graph would be a straight line at 45 degrees to the X-axis with zero intercept. Say, a weather channel predicted a 75% chance of rain on 100 days last year and if, in fact, rain did occur on 75 of those 100 days (75%), this point would lie on the diagonal line, a desired outcome as far as trustworthiness of the model is concerned. If the channel predicted a 20% rain probability on 50 other days and rain had actually occurred on 40 of those 50 days (80% of those days), this point would lie way off the diagonal line and suggests the model is not very trustworthy when it predicts low chances for rain. Deviations of the calibration curve from the diagonal line are indicative of model uncertainty.
• Negative Log-Likelihood – The negative of the log of the probability of observing the training dataset given the model.
• Shannon Entropy or Information Entropy – The level of disorder or the heterogeneity present in the data; in clustering problems, for example, there could be clear boundaries demarcating the data into various classes or impure cases may be present where it is ambiguous whether the data point definitively belongs to a particular class, the fraction of such unresolvable impurities present in the data represents entropy.
• Root Mean Square Error – From the forecasts for the time windows in the testing dataset in the case of time-series forecasting.

Summary

That’s a Wrap. In this first blog of a two-part series on uncertainty, we’ve learned what uncertainty is, how we encounter it in personal as well as business situations, and how we use it in making our decisions. We have learned how data scientists, who develop predictive and insightful AI/ML applications by leveraging data, try to bracket their outputs/insights with uncertainty bounds that allow users to develop a sense for how much credence to place on the model’s outputs and guide them toward suitably integrating the outputs into their decision-making processes. 

Part 2: Uncertainty in AI Domains. In the second part of this uncertainty blog series, we go deeper into the nature of uncertainties encountered in natural language processing (NLP), computer vision (CV), and time series applications. Read Part 2 Now!

About the Author

Special thanks to the contributors and technical reviewers of this article:

• Janette Steets, PhD, Director of Data Science
• Srini Anand, Principal Data Scientist
• Cathy Claude, Director of Marketing

If you liked this article, you might also like:

• Maximizing the full potential of AI with performance and scalability Read article
• Revolutionizing the AI landscape with retrieval-augmented generation (RAG), knowledge graphs, and quantized large language models (LLM) Read article
• Beyond Dashboards: The psychology of decision-driven business intelligence/business analytics (BI/BA) Read article

Sources referenced in this article:

1. Comparison of the effects of imputation methods for missing data in predictive modelling of cohort study datasets. JiaHang Li, ShuXia Guo, RuLin Ma, Jia He, XiangHui Zhang, DongSheng Rui, YuSong Ding, Yu Li, LeYao Jian, Jing Cheng & Heng Guo. BMC Medical Research Methodology, Vol. 24, Art. 41, 2024. https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-024-02173-x
2. Missing Data in Clinical Research: A Tutorial on Multiple Imputation. Peter C. Austin, Ian R. White, Douglas S. Lee, Stef van Buuren. Canadian Journal of Cardiology, 2021 Sep, 37(9), 1322-1331 pp., doi: https://doi.org/10.1016/j.cjca.2020.11.010. https://pmc.ncbi.nlm.nih.gov/articles/PMC8499698/
3. A Baseline for Detecting Misclassified and Out-of-Distribution Examples in Neural Networks, 5th International Conference on Learning Representations, ICLR 2017, Toulon, France. https://arxiv.org/pdf/1610.02136
4. What Uncertainties do we Need in Bayesian Deep Learning for Computer Vision? Alex Kendall and Yarin Gal. 31st Conference on Neural Information Processing Systems, NIPS 2017, Long Beach, CA, USA. https://arxiv.org/pdf/1703.04977
5. Tutorial on Uncertainty Estimation for Natural Language Processing, Adam Fisch, Robin Jia, and Tal Schuster. The 29th International Conference on Computational Linguistics, COLING 2022, Gyeongju, Republic of Korea. https://sites.google.com/view/uncertainty-nlp
6. Can you Trust Your Model’s Uncertainty? Evaluating Predictive Uncertainty Under Dataset Shift. Yaniv Ovadia, Emily Fertig, Jie Ren, Zachary Nado, D. Sculley, Sebastian Nowozin, Joshua V. Dillon, Balaji Lakshminarayanan, and Jasper Snoek. 33rd Conference on Neural Information Processing Systems, NIPS 2019, Vancouver, Canada. https://arxiv.org/pdf/1906.02530
7. Calibration of Pre-trained Transformers. Shrey Desai and Greg Durrett. Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing, pages 295–302, November 16–20, 2020. https://aclanthology.org/2020.emnlp-main.21.pdf
8. Images Credit: Images sourced from Adobe Stock.

About Illumination Works

Illumination Works is a trusted technology partner in user-centric digital transformation, delivering impactful business results to clients through a wide range of services including big data information frameworks, data science, data visualization, and application/cloud development, all while focusing the approach on the end-user perspective. Established in 2006, the Illumination Works headquarters is located in Beavercreek, Ohio, with physical operations in Ohio, Utah, and the National Capital Region. In 2020, Illumination Works adopted a hybrid work model and currently has employees in 20+ states and is actively recruiting.

Careers